Diferencia entre área y perímetro en figuras geométricas
El estudio de las figuras geométricas es fundamental en matemáticas, ya que nos permite comprender y analizar las formas y dimensiones de los objetos en nuestro entorno.
Dos conceptos clave en geometría son el área y perímetro, que nos ayudan a cuantificar y medir las características de estas figuras. Aunque estos términos están íntimamente relacionados con la medida de una figura, es importante comprender que son conceptos diferentes con aplicaciones distintas. En este artículo también exploraremos la diferencia entre área y superficie.
En este artículo, exploraremos en detalle la diferencia entre área y perímetro en figuras geométricas. Discutiremos las definiciones de cada uno, las fórmulas utilizadas para su cálculo, ejemplos prácticos de cómo se utilizan en la geometría, y destacaremos las diferencias clave entre ellos. También abordaremos la diferencia entre perímetro y área para una mejor comprensión.
- Definición de área y perímetro en figuras geométricas
- Métodos de cálculo y fórmulas para el área y el perímetro
- Ejemplos prácticos de cómo se utilizan el área y el perímetro en la geometría
- Diferencias clave entre el área y el perímetro
- Importancia de comprender y calcular correctamente el área y el perímetro
- Conclusión
Definición de área y perímetro en figuras geométricas
En geometría, el área y el perímetro son conceptos fundamentales que describen las características de las figuras geométricas.
Área
El área es la medida de la superficie que ocupa una figura en un plano. Se expresa en unidades cuadradas (por ejemplo, cm², m²). Cada figura tiene una fórmula específica para calcular su área. Es relevante mencionar que el área se enfoca en la cantidad de espacio que cubre una figura, mientras que el perímetro se centra en la medida de su contorno.
Ejemplos:
- Cuadrado:
Área = lado × lado - Triángulo:
Área = (base × altura) ÷ 2 - Círculo:
Área = π × (radio²)
Perímetro
El perímetro es la longitud total del contorno de una figura geométrica. Se mide en unidades lineales (por ejemplo, cm, m). Para calcular el perímetro, se suman las longitudes de todos los lados de la figura. Es importante comprender que la diferencia entre perímetro y área es crucial para aplicar correctamente estas medidas en situaciones prácticas.
Ejemplos:
- Rectángulo:
Perímetro = 2 × (largo + ancho) - Triángulo:
Perímetro = lado₁ + lado₂ + lado₃ - Círculo (circunferencia):
Perímetro = 2 × π × radio
Importancia
El área y el perímetro son herramientas clave para resolver problemas de medición y diseño, y tienen aplicaciones prácticas en ingeniería, arquitectura y la vida cotidiana. Comprender la diferencia entre área y perímetro es esencial para aplicar estos conceptos en situaciones reales.
Métodos de cálculo y fórmulas para el área y el perímetro
Aquí te explicamos los métodos de cálculo y las fórmulas más utilizadas para determinar el área y el perímetro de las figuras geométricas más comunes. Al entender qué es área y perímetro, se facilita mucho más este proceso.
Fórmulas para el Área
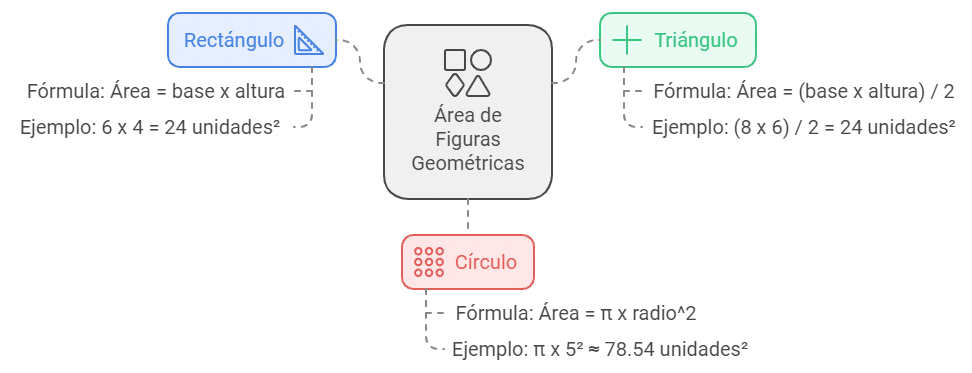
El área mide la superficie de una figura y se expresa en unidades cuadradas como cm² o m². Las fórmulas dependen del tipo de figura.
Figuras y sus Fórmulas de Área:
- Cuadrado:
Área = lado × lado - Rectángulo:
Área = largo × ancho - Triángulo:
Área = (base × altura) ÷ 2 - Círculo:
Área = π × (radio²) - Trapecio:
Área = [(base mayor + base menor) × altura] ÷ 2
Fórmulas para el Perímetro
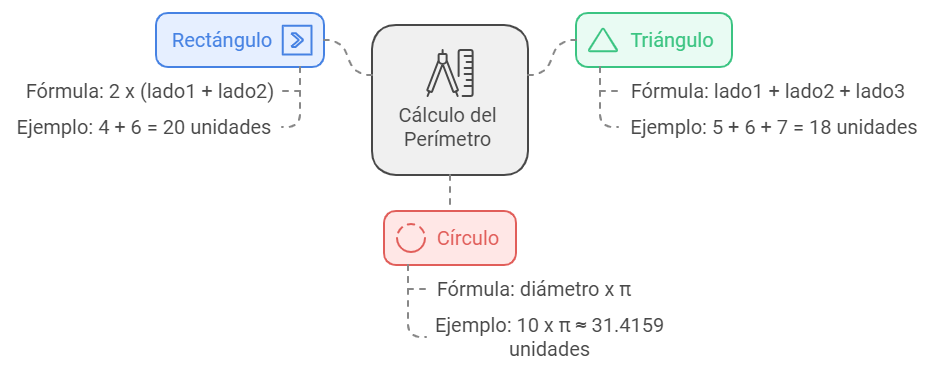
El perímetro mide la longitud del contorno de una figura y se expresa en unidades lineales, como cm o m. Se calcula sumando las longitudes de sus lados o aplicando fórmulas específicas.
Figuras y sus Fórmulas de Perímetro:
- Cuadrado:
Perímetro = 4 × lado - Rectángulo:
Perímetro = 2 × (largo + ancho) - Triángulo:
Perímetro = lado₁ + lado₂ + lado₃ - Círculo (circunferencia):
Perímetro = 2 × π × radio - Polígono regular (con nn lados):
Perímetro = n × lado
Métodos Prácticos de Cálculo
- Medición directa: Usa herramientas como reglas o cintas métricas para medir los lados de figuras reales.
- Aplicación de fórmulas: Sustituye las medidas conocidas en la fórmula correspondiente.
- Estimaciones: Para figuras irregulares, divídelas en figuras más simples y calcula el área o el perímetro de cada parte.
Estas fórmulas y métodos son esenciales para resolver problemas de medición en campos como la geometría, la construcción y el diseño. Conocer qué es área y perímetro ayuda a aplicar correctamente estos conceptos en diversas situaciones.
Ejemplos prácticos de cómo se utilizan el área y el perímetro en la geometría
El cálculo del área y el perímetro tiene aplicaciones prácticas en diversas situaciones de la vida cotidiana y profesional. Aquí se presentan ejemplos concretos de su uso, ilustrando la diferencia entre perímetro y área.
Ejemplos del Uso del Área
- Pintar una pared
Si deseas pintar una pared, necesitas calcular el área para saber cuánta pintura comprar.
Ejemplo:
Una pared mide 4 metros de largo y 3 metros de alto.
Área = largo × alto = 4 × 3 = 12 m². - Cubrir un piso con baldosas
Para cubrir un piso, se necesita calcular el área total del suelo y dividirlo entre el área de cada baldosa para determinar cuántas se necesitan.
Ejemplo:
Un piso rectangular mide 5 m de largo y 2 m de ancho.
Área del piso = 5 × 2 = 10 m². - Diseñar un jardín circular
Si deseas plantar césped en un jardín circular, calculas el área para saber cuánta semilla comprar.
Ejemplo:
El radio del jardín es de 7 metros.
Área = π × (radio²) = 3.14 × (7 × 7) = 153.86 m².
Ejemplos del Uso del Perímetro
- Instalar una cerca
Para cercar un terreno, necesitas calcular el perímetro para saber cuántos metros de material se requieren.
Ejemplo:
Un terreno rectangular mide 10 metros de largo y 8 metros de ancho.
Perímetro = 2 × (largo + ancho) = 2 × (10 + 8) = 36 m. - Colocar molduras en un cuarto
Para decorar una habitación con molduras, necesitas calcular el perímetro de las paredes.
Ejemplo:
Una habitación cuadrada tiene lados de 4 metros.
Perímetro = 4 × lado = 4 × 4 = 16 m. - Bordear un estanque circular
Si deseas instalar un borde de piedra alrededor de un estanque circular, necesitas calcular el perímetro (circunferencia).
Ejemplo:
El radio del estanque es de 5 metros.
Perímetro = 2 × π × radio = 2 × 3.14 × 5 = 31.4 m.
El área y el perímetro son herramientas esenciales para resolver problemas cotidianos relacionados con la construcción, el diseño y la planificación de espacios. Conocer estas aplicaciones permite tomar decisiones informadas en proyectos prácticos, entendiendo la diferencia entre área y perímetro.
Diferencias clave entre el área y el perímetro
El área y el perímetro son conceptos básicos de la geometría que describen diferentes propiedades de las figuras geométricas. Aunque están relacionados, cumplen funciones distintas. A continuación, se presentan sus diferencias clave, además de la diferencia entre perímetro y área que hemos mencionado anteriormente.
Definición
- Área:
Representa la medida de la superficie que ocupa una figura en un plano. Se mide en unidades cuadradas (cm², m², etc.). - Perímetro:
Es la medida de la longitud del contorno de una figura geométrica. Se mide en unidades lineales (cm, m, etc.).
Propósito
- Área:
Se utiliza para calcular cuánto espacio cubre una figura, como el tamaño de una pared, un piso o un terreno. - Perímetro:
Se emplea para determinar la longitud total del borde de una figura, como la cantidad de material necesario para cercar un terreno o colocar un marco.
Fórmulas Básicas
| Figura | Fórmula del Área | Fórmula del Perímetro |
|---|---|---|
| Cuadrado | Área = lado × lado | Perímetro = 4 × lado |
| Rectángulo | Área = largo × ancho | Perímetro = 2 × (largo + ancho) |
| Triángulo | Área = (base × altura) ÷ 2 | Perímetro = lado₁ + lado₂ + lado₃ |
| Círculo | Área = π × (radio²) | Perímetro = 2 × π × radio |
Diferencias en las Aplicaciones
- Área:
- Calcular la cantidad de pintura para una pared.
- Determinar el tamaño del césped necesario para un jardín.
- Cubrir un piso con baldosas.
- Perímetro:
- Medir la longitud de una cerca para un terreno.
- Colocar molduras decorativas alrededor de una habitación.
- Instalar bordes alrededor de un estanque.
Unidades de Medida
- Área:
- Siempre en unidades cuadradas: cm², m², km², etc.
- Perímetro:
- Siempre en unidades lineales: cm, m, km, etc.
Resumen
| Aspecto | Área | Perímetro |
|---|---|---|
| Qué mide | Superficie | Longitud del contorno |
| Unidades de medida | Cuadradas (cm², m²) | Lineales (cm, m) |
| Aplicaciones comunes | Cubrir espacios, medir terrenos | Cercar figuras, decorar bordes |
Ambos conceptos son esenciales en geometría y se aplican de manera complementaria según la necesidad específica. La diferencia entre área y superficie también es importante de considerar en ciertos contextos.
Importancia de comprender y calcular correctamente el área y el perímetro
El conocimiento del área y el perímetro es fundamental en muchas actividades de la vida cotidiana, así como en campos técnicos como la arquitectura, la ingeniería y el diseño. Calcular correctamente estas medidas garantiza resultados precisos y evita errores que podrían generar costos adicionales o problemas funcionales.
Aplicaciones Prácticas
1. Diseño y Construcción
- Área: Es crucial para determinar la cantidad de materiales como pintura, baldosas o césped necesarios en proyectos de construcción.
Ejemplo: Pintar una pared de 20 m² requiere calcular el área para estimar la cantidad de pintura. - Perímetro: Ayuda a medir la longitud necesaria para instalar cercas, bordes o molduras.
Ejemplo: Cercar un jardín rectangular de 40 metros de perímetro requiere esta medida para comprar el material exacto.
2. Gestión de Espacios
- Área: Es útil para planificar el uso eficiente de espacios, como dividir terrenos o asignar áreas en planos arquitectónicos.
- Perímetro: Es importante en el diseño de bordes, caminos o delimitaciones físicas en espacios abiertos.
3. Resolución de Problemas Matemáticos
- La comprensión de estos conceptos es básica en la educación, ya que desarrolla habilidades de razonamiento lógico y matemático.
- Ayuda a resolver problemas geométricos de la vida diaria, como calcular el área de una piscina o el perímetro de un campo.
4. Control de Costos
- Calcular correctamente el área y el perímetro permite optimizar los recursos y reducir desperdicios.
Ejemplo: Comprar baldosas adicionales por errores en el cálculo del área puede aumentar el costo de un proyecto.
Consecuencias de Errores en los Cálculos
- Pérdida de Materiales: Un error en el área puede resultar en material insuficiente o desperdiciado.
- Problemas de Ajuste: Un perímetro mal calculado puede llevar a piezas decorativas o estructuras mal dimensionadas.
- Incremento en Costos: Los errores aumentan los gastos y el tiempo de ejecución de un proyecto.
Beneficios de Comprender estos Conceptos
- Precisión: Garantiza resultados exactos y confiables.
- Eficiencia: Permite optimizar el uso de materiales y recursos.
- Flexibilidad: Facilita la planificación en diversos tipos de proyectos.
Comprender y calcular correctamente el área y el perímetro es esencial para lograr eficiencia, funcionalidad y ahorro en cualquier tarea que involucre geometría. Además, la diferencia entre área y perímetro es crucial para determinar el enfoque correcto en cada situación.
Conclusión
La comprensión de la diferencia entre área y perímetro es fundamental en matemáticas y sus aplicaciones prácticas. Mientras el área nos permite entender el espacio interior de una figura, el perímetro nos ayuda a medir sus límites externos. Asimismo, es importante tener en cuenta la diferencia entre área y superficie para una mayor claridad en los conceptos.
Algunos puntos clave a recordar:
- Las figuras geométricas tienen tanto área como perímetro
- Cada tipo de figura requiere fórmulas específicas para sus cálculos
- Los ejemplos prácticos ayudan a entender mejor estos conceptos
- Las medidas precisas son esenciales para aplicaciones reales
- La correcta aplicación de estos conceptos es vital en diversos campos
El dominio de estos conceptos no solo mejora nuestra comprensión de la geometría, sino que también nos permite resolver problemas prácticos en situaciones cotidianas, desde el diseño de espacios hasta la planificación de recursos.
La habilidad para calcular correctamente áreas y perímetros es una herramienta invaluable en campos como:
- Arquitectura
- Ingeniería
- Diseño de interiores
- Construcción
- Planificación de espacios
Por último, recordemos que la práctica continua con diferentes figuras geométricas y sus medidas nos ayudará a desarrollar una mejor intuición para resolver problemas relacionados con área y perímetro.

Entradas relaciondas